Machine Learning Foundations for Product Managers Wk 3 - Evaluating and Interpreting Models

Technical terms:

Outcomes vs Outputs
Mean Squared Error (MSE)
Mean Absolute Error (MAE)
Mean Absolute Percentage Error (MAPE)
R-squared coefficient
Class imbalance
Confusion Matrix
True Positive Rate (TPR) or Recall or Sensitivity
False Positive Rate (FPR)
Precision
Multiclass Confusion Matrix
Macro Averaged Recall
Macro Averaged Precision
Threshold
Receiver Operating Characteristic (ROC) curve
Area Under the ROC Curve (AUROC)
Precision-Recall (PR) curve
Average Precision (AP) or Area under the PR Curve (AUC-PR)

Defining Metrics for Success

In Data Science parlance, outcomes are generally the business goals you want to achieve - $ per sale, NPS score of satisfied customers.

Outputs are metrics tied to your model and its performance.

Using the right models and outputs for the right problems

If you're trying to predict a continuous numeric value (is there a possibility of a decimal point?), like house prices or temperature, then regression techniques are generally the right approach.

If you're trying to classify something (is this the thing I'm looking for, yes or no?), like detecting spam or disease, then classification techniques would be better.

If you're just trying to get the model to organize random data into similar looking features, then you'll need clustering techniques and etc.

Each set of techniques will have their own way of measuring error and performance.

Predicting a continuous value with Regression techniques

Regression metrics commonly used to evaluate how good a regression model is:

Different error formulas are good at identifying different types of errors.
Mean Squared Error (MSE): Measures the average of the squared differences between predicted and actual values. It's sensitive to outliers.
Mean Absolute Error (MAE): Computes the average of the absolute differences between predicted and actual values. It's less sensitive to outliers.
Mean Absolute Percent Error (MAPE): Represents error as a percentage of the actual value. It's easy to understand but skewed by high percentage errors for low actual values.

The R-squared coefficient measures how well something explains another thing - like the correlation between ice cream sales and how hot it is. A R-squared value of 0 means there's not even a little correlation between the two, whereas a score of 1 means perfect correlation.

And here's where we put the disclaimer that correlation is not causation.

Check out this model with a R-squared value of 0.739

Clearly, this means to buy BUD when Jupiter is further away from Venus. You're welcome for the free investing tip.

Check out even more examples at Spurious Correlations, an internet treasure: http://www.tylervigen.com/spurious-correlations

Detecting something with Classification techniques

Regression techniques work best if you're trying to predict a number, and you want to see what the relationship is between inputs vs your target (e.g. how does temperature affect ice cream sales, if at all?)

It seems like regression methods are fine if you want to ignore outliers and just focus on the patterns of the majority of the samples. But what if the outliers are what matters?

What if you're trying to build a model that can detect something that is rare?

Diseases
Fraud detection
Anomalies like network intrusion, which could be a sign of a cybersecurity threat
Spam mail

In data science speak, if there is a class imbalance then your model shouldn't be using accuracy to judge its performance. As in, the problem has a very large number of 1 class and a very small number of values in another class (aka, the thing I'm actually looking for, the other class, is rare). If you just ran an accuracy test on the model it'll accurately predict that most people do not have heart disease - which is correct, but that is useless.

Use Confusion to Get Clarity

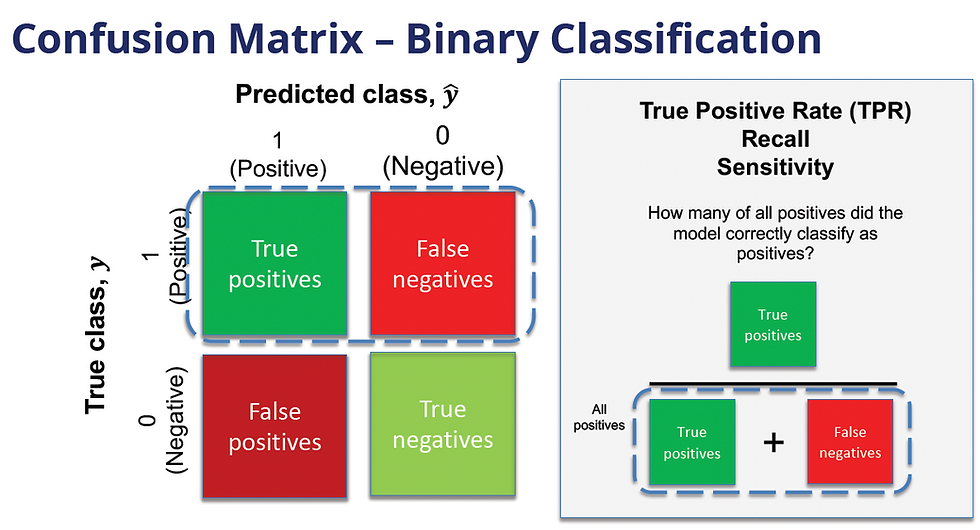
Instead of using accuracy to evaluate if a classification model is doing a good job at correctly detecting things, use a Confusion Matrix

How many true detections (correctly identified positives/these are the droids that I'm looking for) vs false detections (I've incorrectly identified these droids as my target when it's really not - just an error, not a Jedi mind trick)
Below is a chart of what a binary classification (I'm just looking for one thing - yes it is or no it isn't) confusion matrix can look like

True Positive Rate (TPR) or Recall or Sensitivity - how many of the actual positive cases did the model detect?

Accounts for false negatives (this should have been detected as a positive and it wasn't) and true positives

False Positive Rate (FPR) is the inverse of TPR - how many times did the model incorrectly detect a positive that was actually a negative?

Accounts for false positives and true negatives (this really was a negative)

Precision - how many of the model's positive predictions were actually correct?

Accounts for false positives and true positives

What about detecting multiple classes?

Need a model that can detect more than just 1 disease, or identify multiple items in an image, or does more than just identifying 1 thing? Look no further!

Use a multiclass confusion matrix to visualize how the model is doing at detecting different classes. In a multiclass confusion matrix:

Rows represent the actual classes or labels.
Columns represent the predicted classes by the model.
- Each cell in the matrix should be read as 'for row/actual class, how many times did the model predict it as (whatever the column label is)'

The matrix lets you quickly see how well the model is doing at detecting different classes

Let's count flowers - the model in question is being trained on detecting different species of iris flowers - Setosa, Versicolor, and Virginica

I dunno, they all kinda look the same to me.

The image samples the model has been given includes the following:

Setosa - 13
Versicolor - 16
Virginica - 9

In the multiclass confusion matrix, the model was able to do the following:

Positively identify all 13 Setosa flowers - yay!
Positively identify 10 of the Versicolors, but then it falsely identified 6 of the Versicolors as Virginica (well, you have to admit they do look alike)
Positively identify all 9 Virginica flowers - yay!

Not bad! Visualized below is the multiclass confusion matrix for the model:

The same metrics that we used for detecting 1 class can also be used in a multiclass scenario, and calculated for each class (TPR, precision, FPR etc...)

You can even calculate an average across all the classes
Macro Averaged Recall or Macro Averaged Precision - average of all your recall/TPR values from all the classes, or of your precision values from all the classes

That's all for confusion matrices for now! I'm quite positive that the matrix was named after the effect of granting you confusion when you see it for the first time:

More Evaluation/Error Metrics for Classification Models - ROC, AUROC, PR Curves

How confident is your model that what it's looking at is the class that you're trying to identify (e.g. i s it a Setosa, Versicolor, or a Virginica Iris flower)?

Classification models estimate a probability that the sample it's looking at indeed is the class you're trying to identify. But to classify it as such, it needs to have a probability score that is at least as high as the threshold set for it:

Ex if I set my threshold for identifying a Setosa Iris flowers as 0.5, my model has to be able to hit a 0.5 or higher probability score in order to classify that observation as a Setosa
Setting a higher threshold would require the model to have more precision, which can lead to fewer false positives. However, this can lower recall (aka your True Positive Rate/TPR), in that it might miss actual positives in its predictions.
Recall/TPR tells you how many actual positive instances it was able to identify - out of the 13 Setosa flowers that were in the dataset, how many did it manage to identify as Setosa?
Precision is how many of its positive predictions were actually correct vs false positives.

Evaluating models with ROC Curves

So you have thresholds of how well the classifier needs to perform before it can classify something as XYZ. But how do you get around to evaluating classifier models - against each other? Some models may predict certain Iris flowers better than others, but at the end of the day you'll have to pick your top contenders. Which model runs best overall?

Enter ROC curves - get some data on how your models are performing, plot those outputs as dots on a graph, connect those dots (you'll get a curve), then calculate the area under that curve (AUROC or Area Under the ROC curve). The model with the highest AUROC value wins.

Set your threshold - this is up to you
Using the threshold, run the model to get its classifications (was it a positive or a negative outcome)
Calculate your True Positive Rate and False Positive Rates - TPR is how many actual positive instances were classified as positive, and FPR is the rate that the model made false positive predictions (incorrectly classified a negative as a positive)
Change the threshold and repeat this process again. Do it for different threshold values.

You can visualize the outcomes in this chart, where they set thresholds at 0.3, then 0.5 and then 0.7, and plotted this against the model's outputs:

'1' in the grey area means it was a positive classification. You can see how when the Model Output column meets or exceeds the value of the threshold, it gets a '1' - the opposite is true if the output value is below the threshold

The Target column holds the truth - should this have been classified as a positive ('1') or a negative ('0').

Within each threshold column, calculate the TPR and the FPR for ALL of the test outcomes in that threshold. Example:

For Column Threshold = 0.3 the TPR rate
- You can quickly see that there are 2 instances where the Threshold column's positive values matches what's in the Target column; 2 = Numerator
- There were 2 times where the Target column had a positive ('1'); 2 = Denominator
- 2/2 is your TPR
For Column Threshold = 0.3 the FPR rate
- For FPR, there are 2 times the Threshold column's positive values did not match the Target column; 2 = Numerator
- There were 3 times in the Target column that had a negative ('0'); 3 = Denominator
- 2/3 is your FPR
When finding TPR and FPR, we're evaluating how the model is doing at identifying positives, so you're ignoring the fact that in Row 3 of Threshold = 0.7 that the model predicted a a false negative (a positive that was incorrectly classified as negative)

Finally - once you've done this several times you can then plot your FPR and TPR scores on a graph and get a ROC curve.

(I think the one below is mostly for demonstration purposes; these values don't quite look like what you would get if you plot it on a graph).

Yes, this was the highest resolution I could screen capture.

When I throw in the FPR and TPR values in ChatGPT to generate the ROC Curve, this is what it gave me:

To be fair, there wasn't that much data.

TLDR; Higher AUROC = Better Model

At a high level, this is what you're trying to determine - how good is your classifier model?

A perfect classifier will have a TPR/recall of 1 and an FPR of 0 - it'll be able to detect all the positives in the sample, and have no false positives.

A model with a Random classifier performance is like a 50/50 chance of getting the right answer (as good as a coin flip).

The AUROC would roughly 0.5 on a random classifier (the straight line on the chart)

Therefore, a higher AUROC score is a sign of a stronger classifier.

Evaluating with PR/Precision-Recall Curves

Remember how things can get thrown off if you're trying to detect something that is rare (disease, fraud incidents) - or in data science speak, you have a 'class imbalance' where there are lots of certain classes and not much of other ones?

Enter Precision-Recall or PR Curves - because using a ROC curve in this instance would make it 'accurately predict' that 'most of these patients do NOT have heart disease!' and it would be correct. Instead, a PR Curve looks at how well the model is at accurately identifying the thing that it needs to look for (e.g. heart disease).

Precision is the score for how many of the models' predictions are correct, and recall or TPR is a measure of its ability to find all the cases that it's looking for
Creating a PR Curve is similar to creating a ROC Curve - you evaluate the model at different thresholds
This time, you're calculating the Precision and the Recall/TPR scores
Again, plot these things on a graph

The burning question I'm sure most are thinking - is there an Area under the PR curve like there is for the ROC curve (and not, 'how long have I been staring at this page?') Why yes!

Not covered in the course, but can confirm we have an Average Precision (AP) or Area under the PR Curve (AUC-PR)
- Data Scientists aren't exactly the most creative bunch at naming things, it seems
Like with evaluating AUROC values, a AUC-PR of 1 means it's a perfect classifier, and a 0.5 means it's random.
Higher AUC-PR, better classification model

Classify this - is this a good boy? YES HE IS!

If model was designed to assign 'good boy/girl' to any dog, it would be a PERFECT classifier.

When Models are Bad - Troubleshooting Model Performance

There's usually 5 reasons why a model isn't performing well:

Did you frame the problem correctly (which determines whether you're using the right metrics?
1. E.g. is it more important to an electric utility to know how many weather events are happening in a town, or how severe an event is? Turns out, severity was more important than the number of weather events, so in this case you'd want a classification approach (instead of trying to predict a number of events).
Data quantity and quality - does your data have a large number of outliers, is the data unclean?
Feature selection - reach out to your domain experts to help you find the right key features to focus on.
Model fit - If you've done all of the above correctly, then have you tried other algorithms and hyperparameters?
Inherent error - sometimes, the real world problem is just too complicated to model. Even the best models are not 100% accurate.
1. Examples - Human behavior and market dynamics, random 'black swan' events that cause huge and sudden fluctuations - like the COVID pandemic

Probably no model could have ever predicted the great TP shortage of 2020.

Human behavior - throwing a wrench into our prediction models.

Like this post? Let's stay in touch!

Learn with me as I dive into AI and Product Leadership, and how to build and grow impactful products from 0 to 1 and beyond.

Follow or connect with me on LinkedIn: Muxin Li